Just now, the Thinking Machines Lab blog discussed strategy distillation, and Qwen was mentioned 38 times.
default / 2021-11-15
Just now, Thinking Machines Lab (hereinafter referred to as TML)—a team that prefers publishing blogs over papers—updated again with a blog titled On-Policy Distillation.
On-policy distillation is a training method that combines the error-correction relevance of Reinforcement Learning (RL) with the reward density of Supervised Fine-Tuning (SFT). When applying it to mathematical reasoning and internal chat assistants, TML found that on-policy distillation can outperform other methods at an extremely low cost.
Mira Murati, CEO of the company, stated that this method can be used for small models, endowing them with strong domain performance and continuous learning capabilities.
Notably, in this new blog, TML explicitly mentioned that this new achievement was inspired by the research of the Qwen team, and the Qwen3 series models were extensively used in the experimental process. In fact, the keyword "Qwen" appeared as many as 38 times in the original English blog—one more than the 37 times "Apple" was mentioned by CEO Lei Jun at Xiaomi's 17-series press conference.

As a star startup, TML's updates have attracted widespread attention. Some have summarized its advantages:

Netizens even praised TML as the "true Open AI."

The lead author of this blog is Kevin Lu, a researcher at Thinking Machines Lab. Previously, he worked at OpenAI, leading the launch of 4o-mini and participating in the research and development of models such as the GPT-5 series, GPT-oss, o3 & o4-mini, 4.1-nano & 4.1-mini, o1-mini, and o3-mini.
Below, we will take a detailed look at the content of this blog.
Large Language Models (LLMs) can demonstrate expert-level performance in specific domains. This is the result of the combined effect of several capabilities, including: input perception, knowledge retrieval, planning and selection, and reliable execution.
To achieve this, a series of training methods are required, which can be roughly divided into three stages:
Pre-training: Imparts general capabilities such as language use, broad reasoning, and world knowledge.
Mid-training: Teaches domain-specific knowledge such as code, medical databases, or internal company documents.
Post-training: Guides target behaviors such as following instructions, solving mathematical problems, or chatting.
In specific professional fields, small models with intensive training often outperform large general-purpose models. Using small models offers numerous advantages:
They can be deployed locally for privacy or security considerations.
They can be more easily continuously trained and updated.
They also save inference costs.
To leverage these advantages, it is necessary to select the correct methods for the subsequent stages of training.
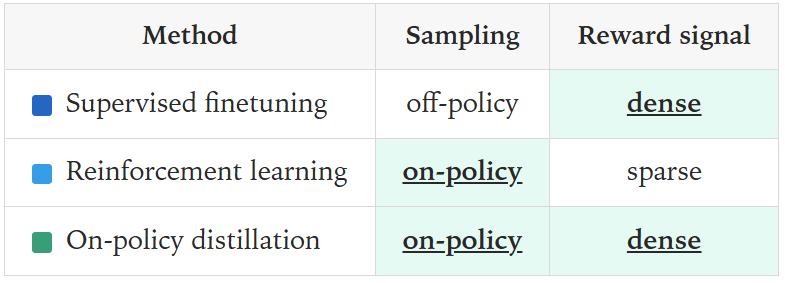
Post-training methods for student models can be divided into two categories:
On-policy training: Samples trajectories from the student model itself and assigns some form of reward to these trajectories.
Off-policy training: Relies on target outputs from an external source, and the student model learns to imitate these outputs.
For example, we may want to train a compact model to solve the following mathematical problem:

We can perform on-policy training through Reinforcement Learning (RL). Specifically, we score each trajectory of the student model based on whether it solves the problem. This scoring can be done manually or by a "teacher" model that can reliably provide correct answers.

The advantage of on-policy training is that students learn to avoid mistakes more directly by training on their own samples.
However, RL has a major drawback: it provides very sparse feedback. Regardless of the number of tokens used, it teaches a fixed number of bits per training episode.
In our example above, the student only knows that "21" is the wrong answer and updates the model to avoid generating that trajectory. But it does not learn exactly where it went wrong—whether it messed up the order of operations or made an arithmetic error itself. This sparsity of feedback makes RL inefficient in many applications.
Off-policy training is usually done through Supervised Fine-Tuning (SFT), i.e., training on a curated set of labeled examples for a specific task. These labeled examples can come from a teacher model that performs well on the current task.
We can use a mechanism called distillation: training the student model to match the output distribution of the teacher model. We train on the teacher's trajectories, which are complete sequences of generated tokens, including intermediate thinking steps.
At each step, we can either use the teacher's full "next-token distribution" (often referred to as "logit distillation") or just sample the given sequence. Practice has shown that sampling sequences provides an unbiased estimate of the teacher's distribution and achieves the same goal. The student model updates its learning for each token in the sequence based on how low the probability of generating that token is (indicated by dark colors in the example below):

Distilling large teacher models has proven to be very effective in training small models, enabling them to:
Follow instructions
Perform mathematical and scientific reasoning
Extract clinical information from medical notes
Engage in multi-turn chat conversations
Distillation datasets for these and other applications are usually open-source and publicly available.
The disadvantage of off-policy training is that students learn in contexts frequently encountered by the teacher, not in contexts they themselves will frequently encounter in the future.
This can lead to compounding error: if the student makes an early mistake that the teacher never made, it will find itself increasingly deviating from the states observed during training.
This problem becomes particularly prominent when we care about the student's performance on long sequences. To avoid this deviation, students must learn to recover from their own mistakes.
Another issue observed with off-policy distillation is that students can learn to imitate the teacher's style and confidence but not necessarily the accuracy of their facts.
To illustrate: If you are learning chess, on-policy RL is like playing chess on your own without a coach. The feedback of winning or losing is directly related to your own moves, but you only receive feedback once per game, and it doesn't tell you which moves contributed most to the outcome. Off-policy distillation is like watching a grandmaster play—you observe highly skilled moves, but these moves are made in board states that novice players rarely encounter.
We hope to combine the on-policy relevance of RL with the dense reward signals of distillation.
For learning chess, this would be like having a teacher score each of your moves, from "terrible" to "brilliant." For the post-training of LLMs, this is on-policy distillation.
The core idea of on-policy distillation is: sample trajectories from the student model and use a high-performance teacher model to score each token of each trajectory.
Returning to our mathematical example above, on-policy distillation would score each step of the solution, punishing incorrect steps that lead the student to the wrong answer while reinforcing correctly executed steps.

In this article, we explore the application of on-policy distillation in the following tasks:
Training models for mathematical reasoning.
Training an assistant model with both domain knowledge and instruction-following capabilities.
We apply on-policy distillation to models that already have basic pre-training and mid-training capabilities. We found that this is a cheap and powerful post-training method that successfully combines the advantages of on-policy training with dense reward signals.
Our on-policy distillation work draws on DAGGER (Ross et al, 2010), an iterative SFT algorithm that includes teacher evaluations of states visited by the student.
It is also similar to Process Reward Modeling (Lightman et al, 2023), an RL method that scores each step in the student model's chain of thought.
We extend the previous on-policy distillation work by Agarwal et al. (2023) and the Qwen3 team (2025). Using the Tinker training API, we replicated Qwen3's results, achieving comparable performance on reasoning benchmarks through on-policy distillation at only a fraction of the cost of RL.
You can follow each step of the implementation in this Tinker cookbook:
On-policy distillation can use various loss functions to score the student's trajectories. For simplicity, we choose token-wise reverse KL (Kullback-Leibler) divergence—i.e., the divergence between the distributions of the student (π_θ) and the teacher (π_teacher) at each token, given the same preceding trajectory:
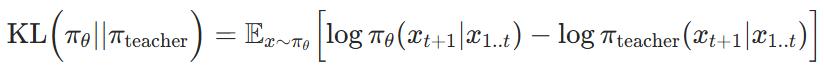
Our reward function minimizes reverse KL, encouraging the student to approximate the teacher's behavior in every state it encounters. When the student's behavior is identical to the teacher's, the reverse KL is zero. For simplicity, we use a discount factor of zero: at any given time step, the student only optimizes for the immediate next token, not future tokens.
Reverse KL naturally synergizes with RL, which typically optimizes some sequence-level reverse KL guided by a reward model. However, unlike most reward models in practice, reverse KL is "unhackable" because low KL always corresponds to high-probability desired behavior from the teacher model's perspective. Another useful property of reverse KL is that it is "mode-seeking"—it learns a specific behavior (the teacher's behavior) rather than spreading its distribution across several suboptimal options.
This approach saves significant computational resources. Because it does not need to wait for a trajectory to be fully sampled to compute the reward, we can use shorter or partial trajectories for training. Querying the teacher's log probabilities also only requires a single forward pass of the large model, while trajectories are generated by the smaller, cheaper student model.
We also do not need a separate reward or annotation model. Combining token-wise distillation-based rewards with sequence-level environmental rewards may be beneficial; this is an interesting potential research area for the future.
Let's look at a real example of an incorrect student trajectory scored by a teacher model. This example is from SimpleBench, which requires the model to make a key observation: the premise of the problem matters. The correct answer is "B. 0" because ice cubes melt in a frying pan. The student model (Qwen3-4B-Instruct-2507) incorrectly treated it as a purely mathematical problem without considering the physical context.

The darker the color, the higher the penalty imposed by the teacher model (Qwen3-235B-A22B-Instruct-2507), which correctly solved the problem.
We see that it penalizes the starting tokens of phrases that led the student astray, which intuitively correspond to important "forking tokens" that guide reasoning. The final answer (though incorrect) was not penalized—because given all the preceding sequences, this answer was completely predictable.
We implemented on-policy distillation on top of Tinker's RL script, which already handles sampling, reward computation, and policy gradient-style training updates.
Initialize the teacher client: The Tinker API can easily create different clients for different models. We use a sampling client because we do not need to propagate log probabilities through the teacher model.
Sample trajectories: We sample trajectories from the student model as in RL. During sampling, RL already computes the student's log probabilities log π_θ(x), which are used as part of the importance sampling loss.
Compute rewards: We query the teacher client on the sampled trajectories using the compute_logprobs function, which returns the teacher's log probabilities log π_teacher (x) over the student-sampled tokens x. We then use this to compute the reverse KL.
Train with RL: We set the token-wise advantage to the negative reverse KL and call RL's importance sampling loss function to perform training updates on the student model.
The pseudocode is as follows:

In the experiments below, we typically apply on-policy distillation to models that have already been trained on domain-specific knowledge. This training increases the probability that the student generates tokens within the teacher's distribution, although this is usually far from sufficient to replicate the teacher's performance. Often, as we will see in the personalization example, the probability of generating relevant tokens starts at zero because the student lacks any relevant domain knowledge.
We will use on-policy distillation for post-training and compare it with other methods for the final critical stage of training expert models.
We used distillation to train the mathematical reasoning capabilities of the Qwen3-8B-Base model, with Qwen3-32B as the teacher model. Both the teacher (Qwen3-32B) and the student (Qwen3-8B-Base) are currently supported on Tinker, so you can replicate our experiments using the Tinker cookbook.
As mentioned earlier, all our experiments start with off-pol